To help the reader out, I’ve posted some helpful files dealing with simulating a LM358 opamp macro from ON semiconductor here.
AC Analysis and Breaking the Loop
The above example shows an AC analysis test-bench GSCHEM. In this example the loop is broken by R3 whose value at dc is 1mΩ and is changed to 1TΩ for ac analysis. Doing this enables NGSPICE to converge on a sensible dc operating point for open loop analysis without any imperfections such as input offset forcing the output to one of the supply rails.
But There are 2 Opamps in this Example!
Indeed there are. One major drawback of AC analysis is that it when the loop is broken, it decouples the loop output from its feedback node. In the case of a MOS opamp for instance, that may have been designed for low noise applications, meaning the input pair is quite large, the input capacitance of the opamp an have a major impact on loop stability when coupled with its output impedance and feedback network impedance. Breaking the loop means the interaction between these two impedances is not simulated. This can create misleading results which will not correlate with a transient analysis on the same circuit.
In order to model this combination of impedances, at least to a first order, we add a second opamp to the output of the first.
Simulating the Loop
In this scenario we netlist the schematic, then create a control file as follows. NGSPICE is run on the control file which sources the schematic netlist. It is not run directly on the netlist.
It is important to leave a free line at the top of the control file. See the download material.
[box style=”1 or 2″ background=”IMG URL or Color Value”]
.control
set sourcepath = ( /projects/student/data/netlist/lm358/ )
source lm358_ac_tb.net
save all
ac dec 20 0.01 1G
let phase=180/PI*vp(vout)
echo “—-”
echo “—-”
meas ac gm_db find vdb(vout) when vp(vout)=0
meas ac pm_deg find phase when vdb(vout)=0
meas ac 3db_f when phase=135
meas ac 0db_f when vdb(vout)=0
meas ac dc_gain find vdb(vout) at=1
echo “—-”
echo “—-”
plot vdb(vout) phase
write /projects/student/data/raw/lm358/lm358ac_tb.raw all
.endc
[/box]
What’s Going On Here?
- Blank line. This is important.
- .control – start of the control file
- set sourcepath – This defines the directory where our netlist lives
- source – This is the netlist we will be simulating.
- save all – Saves all voltage and currents.
- ac dec 20 0.01 1G – Performs an ac analysis, 20 points per decade from 10mHz to 1GHz
- let phase=180/PI*vp(vout) – ac analysis in NGSPICE gives us phase in radians. This line converts the phase at node vout to degrees.
- meas ac gm_db find vdb(vout) when vp(vout)=0 – Find the value of vout in dB’s when phase =0. This last part could be written “when phase =0” The value is stored to gm_db and is our gain margin.
- meas ac pm_deg find phase when vdb(vout)=0 – finds the value of vout phase when vout =0dB and stores it to pm_deg. This is our phase margin.
- meas ac 3db_f when phase=135 – measures the frequency when phase is 135 degrees and stores it to 3db_f. Since the opamp in the test-bench is set up in inverting mode, the “dc” phase is 180°. 180-45=135, so this is our dominant pole.
- meas ac 0db_f when vdb(vout)=0 – measures the frequency when vout crosses 0dB. This is our unity gain frequency.
- meas ac dc_gain find vdb(vout) at=1 – measures the dc gain in dB at 1Hz. This is our dc gain.
- plot vdb(vout) phase – gives us our Bode plot. See below.
- write /projects/student/data/raw/lm358/lm358ac_tb.raw all – writes the simulation data to a file. Useful if we want to look at the data once NGSPICE has closed down.
- .endc – ends the control file
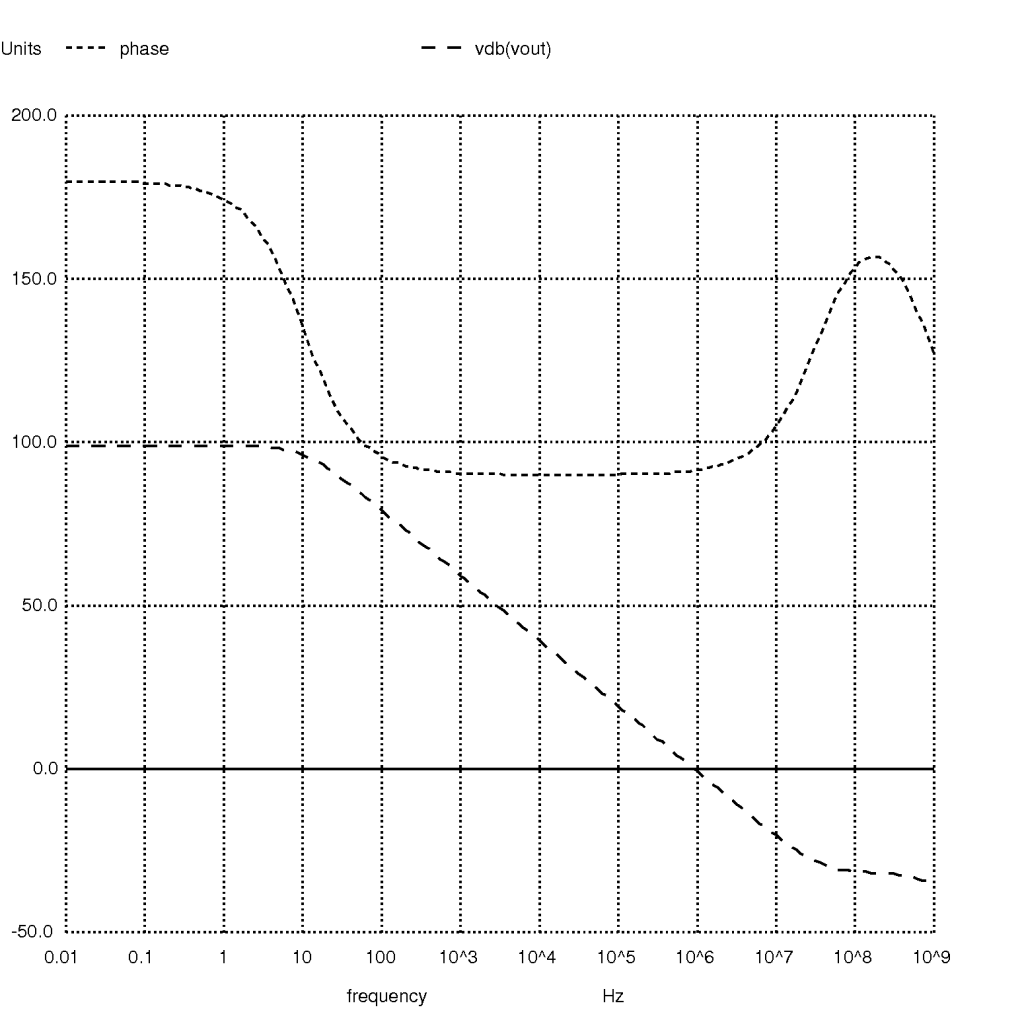
This gives us the following results:
[box style=”1 or 2″ background=”IMG URL or Color Value”]
pm_deg = 9.140923e+01
3db_f = 1.009493e+01
0db_f = 9.142381e+05
dc_gain = 9.908845e+01
Note: We defined gain margin in the measures section, but no gain margin is reported here. Looking at the Bode plot, we see that the phase does not traverse 0° and so gain margin cannot be reported. This is a limitation of the macro-model.
[/box]
But Is There a More Accurate Method?
As it happens, yes. More than one. Back in the early days of my career, I was working on high frequency control systems for the UK defense industry. We needed to know what the open loop response of our amplifier was to ensure it met our design criteria. These amplifiers were discrete, so severing the loop connection as one can do in an ideal SPICE simulation was not possible. What we did was to use a Nichols Chart in reverse.
Nathanial B. Nichols (1914-1997) was one of the original control theory gurus. He was known mainly for his book “The Theory of Servomechanisms” He gave his name the the Nichols chart.
The principle use of a Nichols chart is to derive the closed loop transfer function of a servo system from its open loop behavior. It follows then that one may derive open loop behavior from the closed loop response. It was always tricky drawing closed loop behavior on a Nichols chart…but I digress.
The Middlebrook Method
In 1975 Dr R. David Middlebrook (1929 – 2010) published his seminal paper “Measurement of Loop Gain in Feedback Systems” (International Journal of Electronics, Vol 38, No. 4 pages 485-512, 1975)
In this paper Middlebrook describes mathematically how to derive the open loop transfer function of an amplifier from its closed loop behavior, even if the loop is unstable! Middlebrook was also coming at this from a point of view of determining open loop response in a discrete system, so as in my case above, without the use of a SPICE simulator.
His method was to inject (probe) an ac voltage into the feedback loop, sweep the ac over the frequency range of interest then do the same with an ac current source in the same spot. Armed with the closed loop voltage and current sweep information, one can derive the open loop transfer function. This is easily implemented in SPICE.
The Tian Method
In 2001 Tian et.al. derived an even more robust method of obtaining open loop response from a closed loop system. Middlebrook’s method relies on the ac voltage and current sources being orientated in a specific direction. However, it maybe that the user is interested in backward transmission. Tian’s approach is to use a little more math to derive the open loop response of a system regardless of how the ac probes are orientated.
“Striving for Small-Signal Stability” Circuits and Devices Magazine, IEEE (Volume:17 , Issue: 1 ) pages 31 – 41 Jan 2001.
Using this approach the mainstream SPICE vendors created a stability analysis tool or STB analysis.
Stability Analysis in NGSPICE
As yet stability analysis (STB) is not included in NGSPICE as a stand-alone routine, however, we can use the Middlebrook and Tian (preferred) methods to do the same thing. It’s a little more involved than it would be in a commercial SPICE environment, but it’s the same thing.
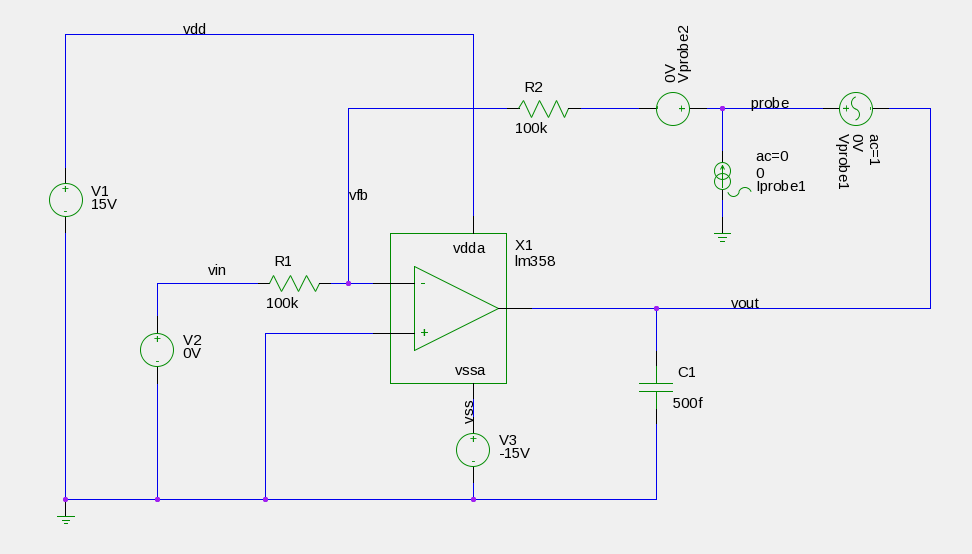
Above is a circuit diagram to carry out our Middlebrook and Tian stability analysis. It’s based on the same opamp macro as before. In this case, since the loop is never broken a second opamp is not necessary to model the closed loop impedance interactions.
In this test-bench, the ac resistor in the previous example is replaced by two voltage sources both of 0V dc (thus the closed loop is maintained) and a 0A ac current source to ground.
We run 2 ac analysis. In the first, we set the ac value of Vprobe1 to 1 and the ac value of Iprobe 1 to zero. In the second the ac values of these 2 sources are reversed.
As in the previous example, we netlist the schematic then create a control file to run in NGSPICE.
It’s important to keep in mind here that unlike ac analysis, stability analysis gives us loop gain as opposed to open loop gain. In the above example, since the ac is injected between the opamp output and the feedback input, the circuit ends up looking like a non-inverting amplifier. In our case, since the feedback network consists of 2 identical resistors, this should look like a gain of 2 – non-inverting rather than 1 – inverting. In this case, the loop gain will be 6dB lower than the open loop gain seen in the ac analysis.
[box style=”1 or 2″ background=”IMG URL or Color Value”]
.control
set sourcepath = ( /projects/student/data/netlist/lm358/ )
source lm358_stb_tb.net
let runs=2
let run=0
alter @Vprobe1[acmag]=1
alter @iprobe1[acmag]=0
dowhile run < runs
set run =”$&run”
set temp = 27
ac dec 20 0.01 1G
write /projects/student/data/raw/lm358/lm358_stb_tb_{$run}.raw all
alter @Vprobe1[acmag]=0
alter @iprobe1[acmag]=1
let run = run + 1
end
let ip11 = ac1.i(vprobe1)
let ip12 = ac1.i(vprobe2)
let ip21 = ac2.i(vprobe1)
let ip22 = ac2.i(vprobe2)
let vprb1 = ac1.probe
let vprb2 = ac2.probe
let mb = 1/(vprb1+ip22)-1
let av = 1/(1/(2*(ip11*vprb2-vprb1*ip21)+vprb1+ip21)-1)
let phase=180/PI*vp(av)
let phase_mb = 180/PI*vp(mb)
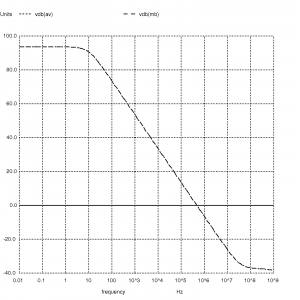
plot vdb(av)
plot phase
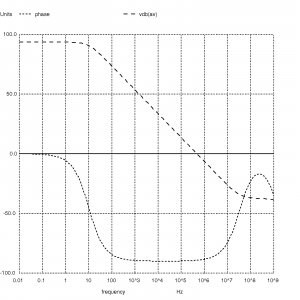
plot vdb(mb)
plot phase_mb
plot vdb(mb) vdb(av)
plot vdb(av) phase
echo “—-”
echo “—-”
meas ac gm_db find vdb(av) when vp(av)=0
meas ac pm_deg find phase when vdb(av)=0
meas ac 3db_f when phase=135
meas ac 0db_f when vdb(av)=0
meas ac dc_gain find vdb(av) at=0.01
meas ac m6dB when vdB(av)=-6
echo “—-”
echo “—-”
.endc [/box]
What’s Going On Here?
- Blank line. This is important.
- .control – start of the control file
- set sourcepath – This defines the directory where our netlist lives
- source – This is the netlist we will be simulating
- let runs=2 – the runs variable will be used to efine how many times we run NGSPICE. In this case 2
- let run=0 – defines the current run number
- alter @Vprobe1[acmag]=1
- alter @iprobe1[acmag]=0 – these 2 lines set up the relevant source the ac simulation will use for analysis. In this case, these lines are not strictly necessary. If you look at the circuit diagram above, you will see that this is how those two sources are set up anyway.
- dowhile run < runs – this sets up a simulation loop. The following lines will loop back to this point as long as the variable runs is less than the variable run
- set run =”$&run” – creates a variable so we know which run is which when we process the results
- set temp = 27 – set the simulation temperature. Irrelevant in this case, but good practice in general
- ac dec 20 0.01 1G – Performs an ac analysis, 20 points per decade from 10mHz to 1GHz
- write /projects/student/data/raw/lm358/lm358_stb_tb_{$run}.raw all – writes the simulation data to a raw file appended by the run number.
- alter @Vprobe1[acmag]=0
- alter @iprobe1[acmag]=1 – as per lines 7 and 8 This swaps the sources the ac analysis will use for the second run
- let run = run + 1 – increments the run number for the loop
- end – ends the loop
- let ip11 = ac1.i(vprobe1)
- let ip12 = ac1.i(vprobe2)
- let ip21 = ac2.i(vprobe1)
- let ip22 = ac2.i(vprobe2)
- let vprb1 = ac1.probe
- let vprb2 = ac2.probe – these lines are added to make the later math simpler to write
- let mb = 1/(vprb1+ip22)-1 – this defines the Middlebrook open loop response
- let av = 1/(1/(2*(ip11*vprb2-vprb1*ip21)+vprb1+ip21)-1) – this defines the Tian open loop response
- let phase=180/PI*vp(av) – defines the phase of av in degrees
- let phase_mb = 180/PI*vp(mb) – defines the phase of mb in degrees
- plot vdb(mb) vdb(av) – plots the Middlebrook and Tian voltage gain in dB on the same axis
- plot vdb(av) phase – a Bode plot of the Tian method
- meas ac gm_db find vdb(av) when vp(av)=0 – finds the voltage gain when the phase goes through zero – our gain margin
- meas ac pm_deg find phase when vdb(av)=0 – measures the phase in degrees when av = 0dB – our phase margin
- meas ac 3db_f when phase=-45 – measures the frequency where the phase goes thought -45° – This is our dominant pole
- meas ac 0db_f when vdb(av)=0 – measures the frequency where the loop gain goes through zero. Since this is loop gain and not open loop gain, this will not be the same as the ac example above.
- meas ac dc_gain find vdb(av) at=0.01 – measures the loop gain. This should be 6dB lower than the ac example
- meas ac m6dB when vdB(av)=-6 – measures the frequency where the gain curve goes below -6dB. This should be the same as the unity gain bandwidth in the ac example
- .endc – ends the control section
This gives us the following results:
[box style=”1 or 2″ background=”IMG URL or Color Value”]
pm_deg = -8.923940e+01
3db_f = 9.988710e+00
0db_f = 4.779122e+05
dc_gain = 9.358252e+01
m6db = 9.538196e+05
Note:
- As per the ac analysis earlier, we cannot measure gain margin
- You will notice some subtle differences. The less accurate ac analysis gave us a phase margin of 91.4°. The more accurate Tian method reports 89.23°
- As expected dc gain is 6dB less than the ac analysis
- 0dB frequency is not the same as in the ac case, since in this case 0dB is where the loop gain goes through zero. Given that the closed loop gain is 6dB, then the point at which the gain curve goes through -6 should correspond to the ac analysis 0dB frequency. Again, due to inaccuracies in the ac method, we do see a slight difference here.
[/box]
This example was derived from work originally carried out by Frank Wiedmann which you can find at https://sites.google.com/site/frankwiedmann/loopgain. Of particular interest is a breakdown of the math used in Middlebrooks general feedback theorem which you can find here.
Special thanks to Robert Larice for invaluable help with the NUTMEG language in NGSPICE.
[profile name=”Justin Fisher” role=”CEO Ingenazure LLC” twitter=”https://twitter.com/ingenazure” facebook=”https://www.facebook.com/ingenazure” linkedin=”https://www.linkedin.com/pub/justin-fisher/1/255/273″ ]Ingenazure LLC[/profile]

One reply on “AC and Stability Analysis in NGSPICE.”
good info, however i need stability information for differential circuits supported in Spectre using CMDM probe.
(ref https://pdfs.semanticscholar.org/c1dc/91d09c4112cf9aab8baefcc345bd2141fcdd.pdf)